·        LE PREMIER MATHEMATICIEN DE L’HISTOIRE

Thalès ne s’est pas beaucoup occupé des nombres, il s’est surtout intéressé aux figures géométriques, cercles, droites, triangles. Il fut le premier à considérer l’angle comme un être mathématique à part entière et fit la 4^ème grandeur géométrique (longueur, surface, volume, angle).

La grande innovation de Thalès réside dans le fait qu’il affirme des vérités, non pas à partir d’un objet singulier, comme c’était le cas avant lui pour les Egyptiens ou les Babyloniens, mais pour une infinité d’objets du monde. Son ambition, d’une nouveauté absolue, est d’émettre des vérités concernant une classe entière d’être.

Pour pouvoir y parvenir, Thalès va être obligé, par sa seule pensée, de concevoir un être idéal, « le cercle », qui est en quelque sorte le représentant de tous les cercles du monde. De ce fait une phrase comme « toute droite passant par le centre d’un cercle le coupe en deux parties égales » est alors révolutionnaire.

C’est en ce sens que l’on peut lui attribuer le titre de premier mathématicien de l’histoire

·        SES APPORTS MATHEMATIQUES

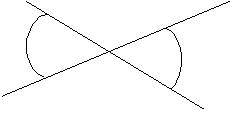
  Thalès affirma que les angles opposés par le sommet formés par deux droites qui se coupent sont égaux.

  
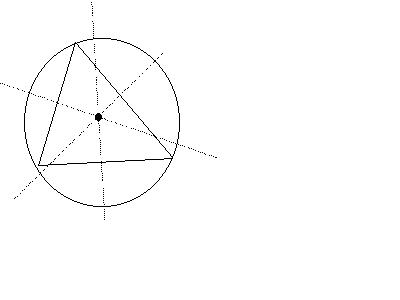
-  Thalès a montré qu’à chaque triangle   on pouvait faire correspondre un cercle,   le cercle circonscrit, dont il a

proposé une construction générale.

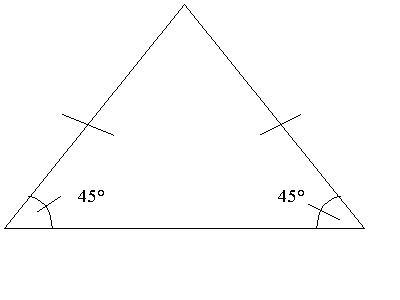
-   Il a démontré qu’un triangle isocèle    avait deux angles de même mesure.

-Thalès propose en outre le « fameux Théorème de Thalès » qui lui permit de mesurer la pyramide de Kheops.

La première démonstration de ce théorème est cependant à attribuer à Euclide (4^ème-3^ème av J C ) qui la présente dans ces « éléments ».

Propriété (ou théorème) de Thalès, que connaissaient les babyloniens : si trois droites parallèles rencontrent deux droites(d) et (d’), respectivement et dans cet ordre, en A, B, C et A’, B’, C’, alors :

A'B'   =  B'C'  =  A'C'

                                                                             AB         BC        AC

En d’autres termes :

Trois droites parallèles déterminent sur deux sécantes(quelconques) des segments homologues proportionnels

Cette proportion fondamentale permettra de résoudre de nombreux problèmes de construction (architecture et géométrie).

Inversement, l’égalité des deux premiers rapports assure le parallélisme des droites (d) et (d’) se coupent en un point donné du plan est étudié dans les classes de 4^ème et 3^ème des collèges :

Il est facile (et intéressant) de vérifier géométriquement que l’ensemble des nombres constructibles, est un sous-corps de R (corps des nombres réels) contenant le corps Q des rationnels.

Rappelons qu’un nombre est dit constructible si, dans un repère du plan. Par point constructible, on entend « à la règle et au compas » comme le voulait Euclide et Platon.

·       Une droite est constructible si deux de ses points le sont.

·        Un cercle est constructible si son centre (point) est constructible et si son rayon (nombre) l’est aussi

Par exemple, se donnant a et b constructibles, on construira leur produit ab (ci-avant)en écrivant la proportion :

 
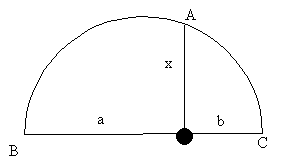
 On pourra aussi facilement construire une moyenne géométrique, c’est à dire un nombre X tel que      = ab où a et b sont des nombres constructibles donnés : on sait en effet que dans un triangle rectangle ABC de hauteur AH, on a :

On a là : x = AH, a = HB et b = HC.

On construit alors un segment [BC] tel que BC = BH + HC.

On trace le demi-cercle supérieur de diamètre BC.

La droite perpendiculaire à [BC] passant par H coupe le demi-cercle en A.

 On a : x = AH car le triangle ABC est rectangle en A :

Le corps C des nombres constructibles est stable par passage à la racine carrée : si X appartient à C , alors la racine carrée de X est aussi élément de C.

On dit que C est un corps pythagoricien (appellation en hommage à Pythagore qui « découvrit » les nombres irrationnels. A noter que C est aussi le plus petit corps pythagoricien inclus dans R)

page précédente   page suivante