LE MIRLITON D'ARCHIMEDE
Comment mesurer l'aire d'un disque ?
Archimède est le premier a avoir
expliqué comment calculer, l'aire d'un disque lorsque
l'on connaît le périmètre du cercle qui le délimite.
Voici les étapes de son raisonnement
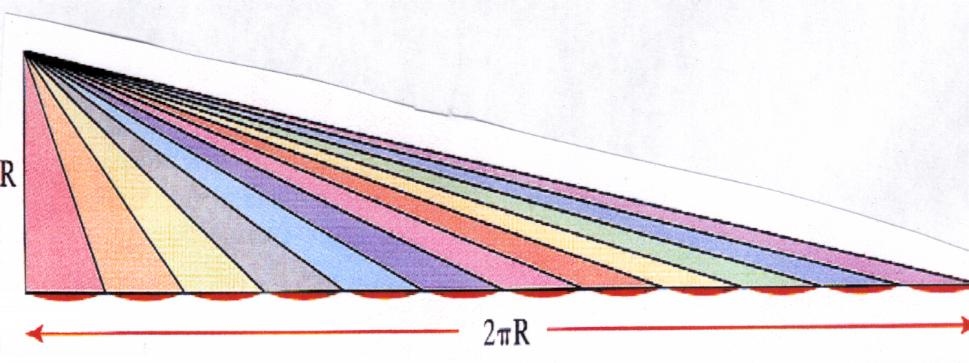
1) Découper un cercle en beaucoup de triangles.
2)
Souffler dans le mirliton obtenu de
manière à aligner les base des triangles.
Tous ces triangles ont la même hauteur ( presque égale au rayon
du cercle ) ont ensemble la même aire que le triangle de hauteur ( presque
égale à ) R et de base
( presque ) le périmètre du cercle soit 2¶ R
En effet en déplaçant le sommet de chaque triangle parallèlement à la base, on ne change pas son aire.
L?aire du grand triangle de hauteur R et de base 2 ¶R est donc très peu différente de :
½ ( 2 ¶R ) ![]() R
soit ¶ R²
R
soit ¶ R²
L'aire du disque ne peut donc différer de ¶ R² que d'une petite différence. Mais cette différence peut être rendue aussi petite que l'on veut .
L'aire du disque vaut donc exactement ¶ R²